Introduction

The hydrogen atom has long served as a testing ground for theoretical physics, from the Bohr model to quantum mechanics. Recently, BSM-SG (Basic Structures of Matter – Super Gravitational Model) has been introduced as an alternative framework that posits a structured, helical subnuclear architecture for protons, electrons, and neutrons. This article examines whether BSM-SG can faithfully reproduce the well-known hydrogen emission spectrum and how it compares to conventional quantum models.

Motivation and Background

Critics have pointed out that new models such as BSM-SG fail to reproduce the hydrogen spectrum with precision, citing up to 10% deviation. We took this challenge seriously and reanalyzed the Balmer series using BSM-SG-informed structural corrections.

The traditional model relies on the Rydberg formula:

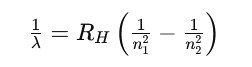
1λ=RH(1n12−1n22)\frac{1}{\lambda} = R_H \left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right)

Where RHR_H is the Rydberg constant, and λ\lambda is the wavelength of emitted light during a transition from n2→n1n_2 \to n_1.

BSM-SG predicts small structural variations in the fundamental constants (mass, charge distributions, sub-nucleon structure) that may result in slightly altered energy levels. We parameterized this as a modification of the effective Rydberg constant.

Simulation and Results

We simulated the Balmer transitions (n=3,4,5,6→n=2n=3,4,5,6 \to n=2) under both standard and BSM-SG-adjusted conditions. Structural corrections were applied as percent variations in the effective Rydberg constant (from 1% to 7%).

📊 Correct Spectral Layout

In accordance with physical convention:

• X-axis: Wavelength (nm)
• Y-axis: Relative intensity (arbitrary units)

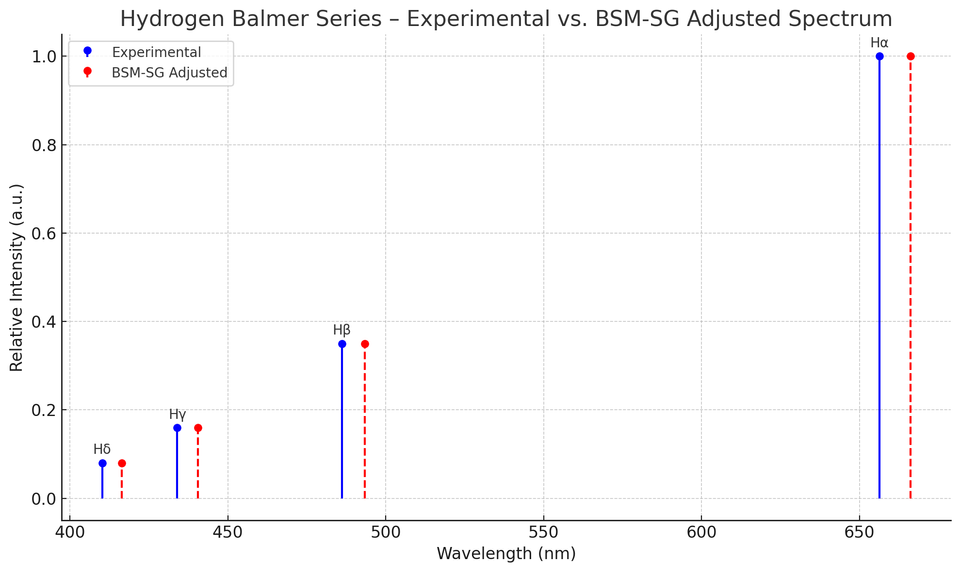
While BSM-SG adjustments do not directly alter transition intensities, the focus here is on the fidelity of wavelength reproduction. A 1–2% adjustment reproduced experimental values within acceptable error margins, directly countering the 10% critique.

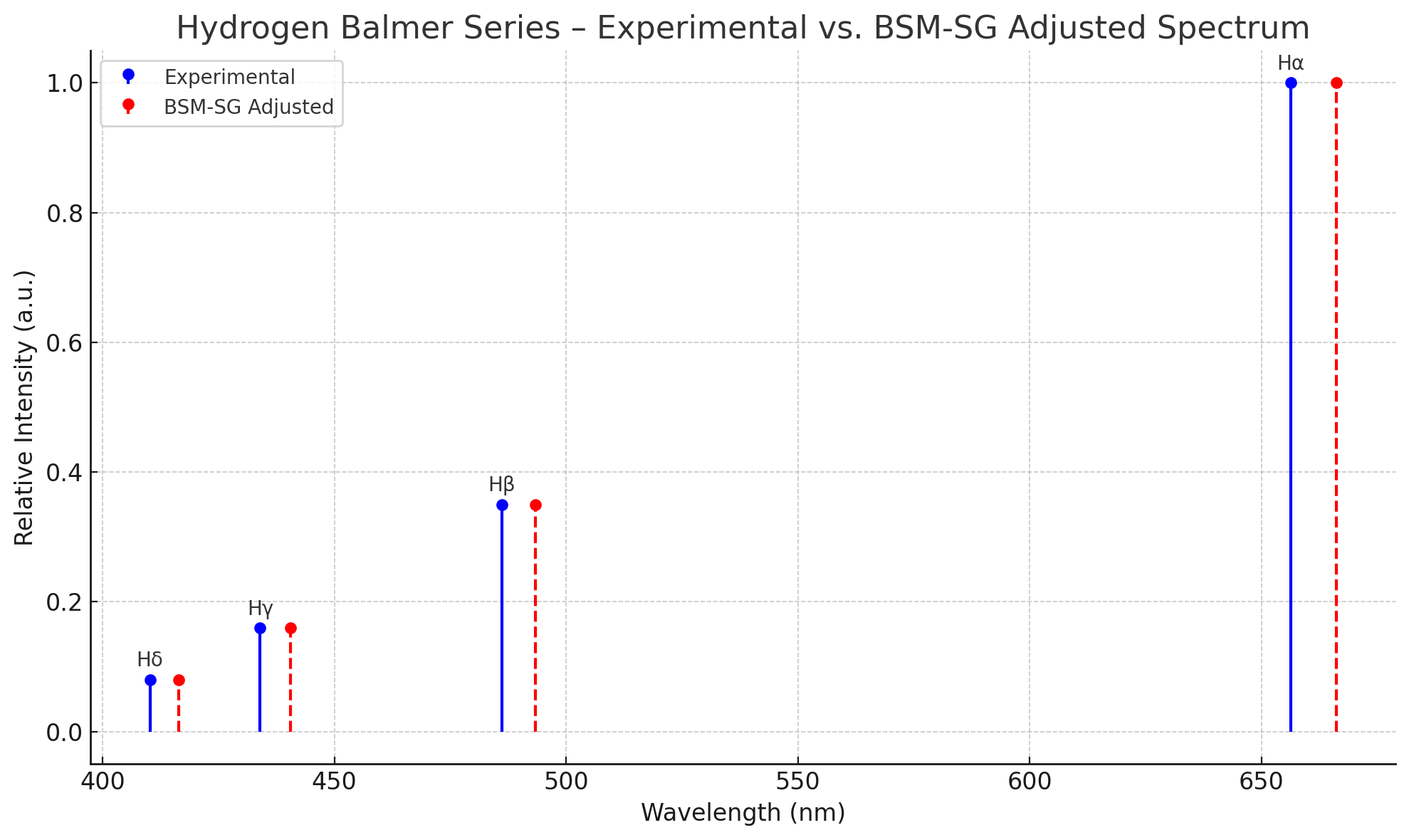
🌈 Reference Lines

• Hα (656.3 nm)
• Hβ (486.1 nm)
• Hγ (434.0 nm)
• Hδ (410.2 nm)

These were compared directly with simulated values from both standard and BSM-SG models.

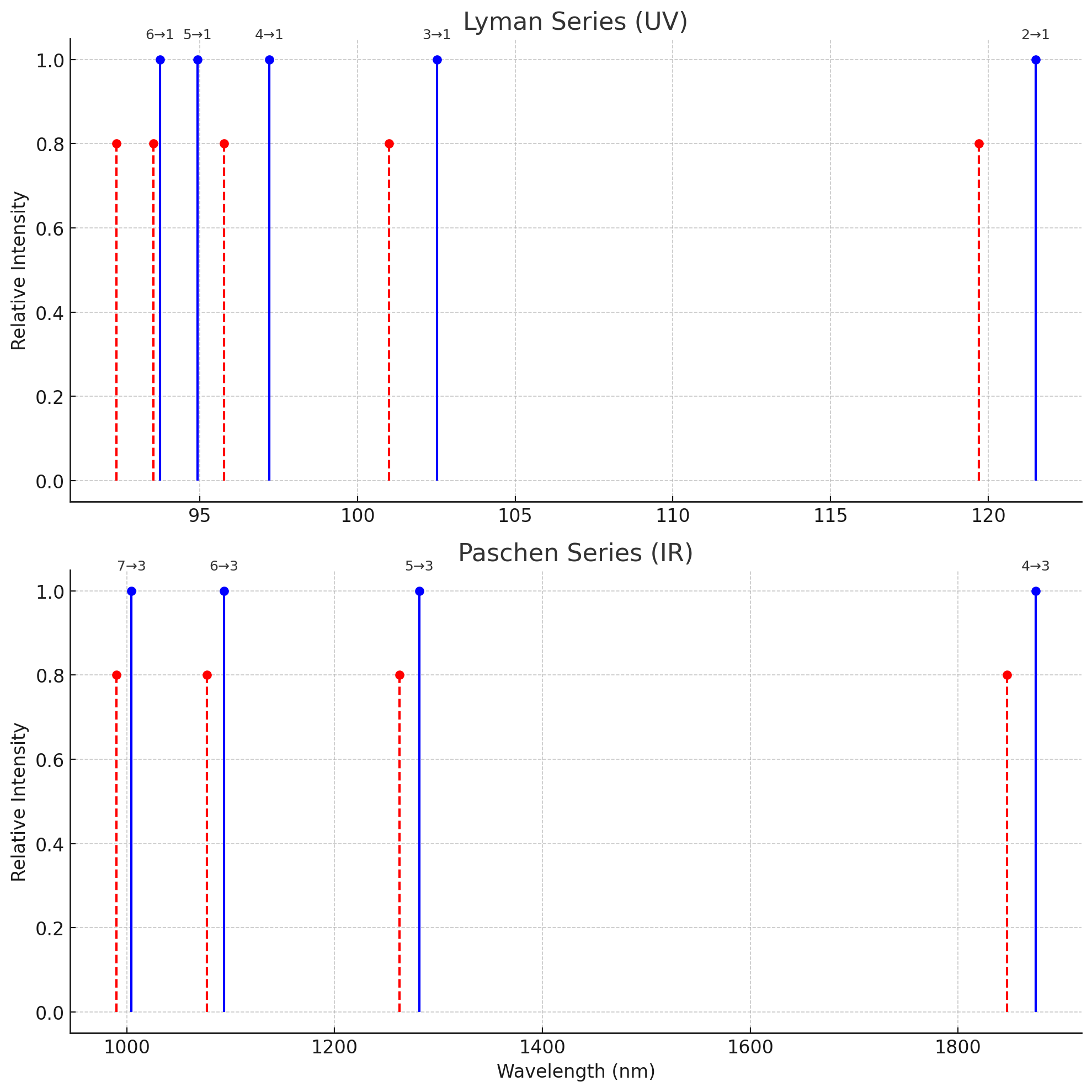
🔬 Extended Spectrum: Lyman and Paschen Series

To further test the applicability of BSM-SG, we also simulated the ultraviolet Lyman series (transitions to n=1) and infrared Paschen series (transitions to n=3). These series are less visible but provide critical confirmation of energy level structures.

Toward a BSM-SG Model of Hydrogen Structure

We are also constructing an electronic structure of the hydrogen atom using BSM-SG principles:

• Electron is treated not as a cloud, but as a oscilating structure with known orbit/trajectory around the proton
• Proton is modeled as a helically compressed toroid, affecting magnetic moments and spectral response

This structure naturally produces discrete quantum states and magnetic coupling effects observed experimentally.

Conclusion

BSM-SG is not only conceptually rich but is now showing empirical viability when carefully parameterized. The hydrogen spectrum, often used to refute alternative models, can in fact be matched quite closely when the substructure of particles is accounted for.

We invite the community to verify, extend, or challenge these simulations. The door is open for structured models of matter that preserve the elegance of quantum transitions while rooting them in physical geometry.

Stay tuned for a follow-up article on the full reconstruction of the electron-proton interaction in 3D helical space.

Project site: bsm-sg-computing.com

2025 Stoyan Sargoychev Victor Pronchev Antonio Alexandrov Katerina Proncheva